
Cost of Capital Professional Frequently Asked Questions (FAQs)
Thank you for visiting the FAQ page for the Cost of Capital Professional platform. If you're unable to find the answer you are looking for, please contact us at 1-503-479-8200 or customerservice@bvresources.com and we are happy to help.
Q: What is the legend for general information?
Company Name | The name of the subject company being valued. This information will be used in the summary output. |
Valuation Date | The valuation date for the assignment. The valuation date is used for providing information for risk-free rate, equity risk premium, size premium, and industry risk premium. (Please see “Returns Reference – End Date," “Treasury Constant Maturity,” and "Industry Beta Selection" below.) |
Returns Reference – Start Year | The starting year used to calculate the historical equity risk premium and historical size premium. The analyst may select from the earliest year available (1928) or another year for the analysis. |
Returns Reference – End Year | The ending year to calculate the historical equity risk premium and historical size premium. The user’s choice for “Valuation Date” determines the options presented. Please see FAQs below for more information. |
Q: What is the legend for the risk-free rate information?
U.S. Treasury Bond Constant Maturity – 20-Year | The spot yield on the 20-year U.S. Treasury bond based on the specified valuation date. The information is retrieved from the Federal Reserve, the U.S. central bank. |
U.S. Treasury Bond Constant Maturity – 10-Year | The spot yield on the 10-year U.S. Treasury bond based on the specified valuation date. The information is retrieved from the Federal Reserve, the U.S. central bank. |
Custom Risk-Free Rate | A custom risk-free rate entered by the analyst. Any notes associated with a custom risk-free rate may also be entered. |
Q: What is the legend for the equity risk premium (ERP) information?
CRSP – Historical ERP | The historical ERP computed as the average difference between the average annualized monthly total return of CRSP’s S&P 500 Universe (500 stocks since March 1957 and 90 stocks prior) value-weighted and the annualized monthly total return for the 10-year U.S. Treasury or the 20-year U.S. Treasury. Sourced from the Center for Research in Security Prices (CRSP). |
Damodaran – Implied ERP | A forward-looking ERP based on the analyst’s “Returns Reference – End Date,” sourced from Dr. Aswath Damodaran. Please see below FAQs for more information. |
Damodaran – Implied ERP With Sustainable Payout | A forward-looking ERP based on the analyst’s “Returns Reference – End Date,” sourced from Dr. Aswath Damodaran. Please see below FAQs for more information. |
Damodaran – Historical ERP | The historical ERP based on the analyst’s “Returns Reference – Start Date” and “Returns Reference – End Date,” sourced from Dr. Aswath Damodaran. |
Custom ERP | A custom ERP entered by the analyst. Any notes associated with a custom ERP may also be entered. |
Q: What is the legend for the CRSP sizes premium information?
Decile | Organized by 1 = Largest to 10 = Smallest, these deciles represent 10 portfolios created by the Center for Research in Security Prices (CRSP) based on market capitalization as a measure of firm size. This measure for firm size has been used widely in academic research. The CRSP methodology for decile formation uses the universe of common stocks of eligible companies listed on the NYSE, NYSE MKT, and Nasdaq National Market. The universe omits unit investment trusts, closed-end funds, REITs, Americus Trusts, foreign stocks, and American Depository Receipts. Eligible companies trading mainly on NYSE are ranked into equally populated deciles. The largest capitalizations in each decile are the breakpoints for decile assignment for all eligible companies on all exchanges. Eligible NYSE MKT and Nasdaq National Market firms are then assigned to deciles based on these breakpoints. This practice is used frequently in academic research. |
Min Size/Max Size ($000) | These represent the breakpoints for the decile for the selected Returns Reference – End Year. The breakpoints shown are the minimum market capitalization and maximum capitalization of firms by the “Returns Reference – End Year. |
Count | The number of firms in the decile by the “Returns Reference– End Year.” |
Annual Return | The average annualized monthly common stock total return of firms in the decile over the historical period specified by the “Returns Reference – Start Year” and “Returns Reference – End Year.” Annual return information has been derived from CRSP monthly return data. Arithmetic average monthly returns have been annualized using the standard procedure: ((1+ Monthly return)^12) -1. |
Size Premium (S&P 500) | The historical size premium of the referenced portfolio relative to the S&P 500 portfolio over the selected time horizon. Computed as average annualized monthly decile total return minus the average annualized monthly total return of CRSP’s S&P 500 Universe (500 stocks since March 1957 and 90 stocks prior) value-weighted over the historical time period specified by the “Returns Reference – Start Date” and “Returns Reference – End Date.” Annual return information has been derived from CRSP monthly return data. Arithmetic average monthly returns have been annualized using the standard procedure: ((1 + Monthly return)^12) - 1. |
| Size Premium (Beta Adjusted) | The historical size premium of the referenced portfolio in a CAPM framework over the selected time horizon. The framework is Ri = Rf + (ERP x portfolio beta) + size premium. The size premium (S&P 500) is adjusted by the corresponding portfolio beta over the historical time period specified by the "Returns Reference - Start Date" and "Returns Reference - End Date." Sometimes referred to as the size premium "in excess of CAPM," this measure of size premium has been used with the capital asset pricing model when estimating a cost of equity (sometimes referred to as the "modified CAPM"). Computed as "Size Premium (Beta Adjusted)" = "Size Premium (S&P 500)" - ((ERP x portfolio beta) - ERP). |
Q: What is the legend for the Industry Risk Premium (IRP) information?
A:
| Industry Beta Source | The source of the levered industry betas available to be used in the IRP calculation, based on the user’s valuation date. The available options include Salvidio & Partners and Dr. Aswath Damodaran. |
| Industry Beta Selection | The levered betas available by industry/sector based on the selected Industry Beta Source. Salvidio & Partners industry betas are available for valuation dates from 2018 through current. Dr. Damodaran's industry betas are available for valuation dates from 1999 through current. A custom industry beta may also be entered by the analyst. Any notes associated with the selected industry beta may also be entered. |
| Industry Risk Premium | The implied IRP based on the analyst’s selected industry beta or custom industry beta. Computed as implied Industry Risk Premium = (industry beta x ERP) - ERP. |
Q: What is the source of the data used in the Cost of Capital Professional platform?
A: The spot risk-free rate information (10-year and 20-year Treasury bonds) for the relevant valuation data is sourced from the Federal Reserve.
The information for the CRSP ERP and CRSP Size Premiums is sourced from the Center for Research in Security Prices of the University of Chicago except pre-1942 T-bond return data described below.
Historical returns on risk-free assets (10-year and 20-year Treasury bonds) after 1941 are sourced from CRSP. Prior to the early 1940s, CRSP does not provide T-bond return data because T-bonds before that time had different tax characteristics than T-bonds since then. Prior to 1942, we source T-bond returns from Dr. Aswath Damodaran’s data library where he provides returns on 10-year T-bonds. Prior to 1942, for 20-year T-bond returns, we reconstruct returns from the 10-year returns adjusted for the historic return difference between 10-year and 20-year T-bonds reported by CRSP.
The implied ERP, implied ERP with sustainable payout, and the Damodaran historical ERP are sourced from Dr. Aswath Damodaran’s data library at New York University.
The levered industry beta information are sourced from Dr. Aswath Damodaran's data library and Salvidio & Partners data library. You can learn more about the Salvidio & Partners beta methodology in their recently published report.
Dr. Aswath Damodaran’s data are used with his permission. Dr. Aswath Damodaran has no formal role or connection with BVR or the Cost of Capital Professional. Salvidio & Partners data are used with permission.
Q: Is the Cost of Capital Professional platform a “black box”?
A: Absolutely not. The user will see the CRSP decile size premium table, as well as the calculations for the historical ERPs and size premiums.
Q: The Cost of Capital Professional allows me to choose my start year for which my equity risk premium and size premium are measured. Why is this, and which start year should I choose?
A: The Cost of Capital Professional was created to empower analysts with objective data and a flexible platform. From the platform information, the analyst still needs to apply professional judgment, which may include choosing the period of historical returns to use. According to theory, risk premiums in cost of capital models are forward looking. They represent components of what investors expect to receive as asset returns. If using historical returns to estimate investor expected returns, choose the part of history that you believe best represents investor expectations of the future by first choosing a starting year of historical return data.
When using historical return data for an analysis, the practitioner will decide on a segment of history he or she believes offers a reasonable basis to make estimates of expected future returns by first choosing a starting year of historical return data. Some analysts might start with the earliest year of data available presumably with the belief that the future will resemble the average return of many past decades (over 90 years if starting in the 1920s). Other analysts might start with 1963 because that is the first full year when Compustat started its database. Other analysts might start with 1982, the first year after Rolf Banz documented the size effect in stock returns; other empirical research shows the size premium in listed firms has changed since it was first documented. Alternatively, the practitioner can choose another starting year.
Q: Why is the first start year 1928 instead of 1926?
A: The Cost of Capital Professional uses 1928 because this is the earliest date for data provided by Dr. Damodaran, and we wanted his data to align with the data provided by CRSP. Whether one starts with 1926 or 1928, average returns over 90 versus 92 years change very little.
Q: How often is the information for risk-free rates, ERPs, size premiums, and industry risk premiums updated?
A: The provided risk-free rate information is updated each trading day. The CRSP ERP and Size Premium information are updated quarterly. The ERP information provided by Dr. Aswath Damodaran is updated annually.
While CRSP provides data updates frequently, our ERP and size premium calculations are annual because components in some calculations use data updated only annually. The Cost of Capital Professional applies quarterly CRSP data refreshes for any changes that CRSP makes to its year-end data for any missing data or error corrections. Although CRSP error corrections to its historical data are likely rare, we want to provide the best information possible by having quarterly CRSP data refreshes.
The industry beta information that is used for the implied industry risk premium calculation from Dr. Aswath Damodaran and Salvidio & Partners are updated annually.
Q: What is “Size Premium (Beta Adjusted)” and how does it differ from “Size Premium (S&P 500)”?
A: The Size Premium (S&P 500) is computed as the average annualized monthly decile return minus the average annualized monthly return of the S&P 500. In a capital asset pricing model framework to estimate cost of equity, the Size Premium (S&P 500), implies a beta of 1.0 (assuming the S&P 500 is the proxy for the CAPM market portfolio). CRSP deciles have decile betas relative to the S&P 500 beta of 1. The table below is a general reference for the average historical decile betas from 1926 to 2017.
Decile | 1926-2017 |
1 - Largest | 0.92 |
2 | 1.03 |
3 | 1.10 |
4 | 1.12 |
5 | 1.16 |
6 | 1.17 |
7 | 1.25 |
8 | 1.30 |
9 | 1.33 |
10 - Smallest | 1.39 |
The Size Premium (Beta Adjusted) is the historical size premium adjusted for the decile beta over the selected time period. In the CAPM framework to estimate the cost of equity, when a decile beta is greater than 1.0, beta absorbs some of the Size Premium (S&P 500), where the benchmark S&P 500 has a beta of 1.0. Consequently, beta-adjusted size premiums will be lower than size premiums relative to the S&P 500 when decile betas are greater than 1.0.
Using the equation shown below, Ri is firm i’s cost of equity. Holding the Ri constant, when beta is higher, the size premium is lower. The Size Premium (S&P 500) measure implies beta is 1.0, while the Size Premium (Beta Adjusted) measure does not. If a decile beta is greater than 1.0, the size premium is lower holding Ri constant.
Ri = Rf + (ERP × beta) + SP
Q: When using the buildup model (BUM), should I use the “Size Premium (S&P 500)” or the “Size Premium (Beta Adjusted)”? Is the decision dependent on whether I’m using an industry risk premium (IRP) or not?
A: If the analyst decides to use a size premium, then the “Size Premium (S&P 500),” which is not beta-adjusted, may be appropriate for the buildup model in estimating cost of equity.
Further, the decision to use the “Size Premium (Beta Adjusted)” when using BUM in conjunction with an IRP cannot be generalized too much and would be logical only if the analyst believes risky industries, as measured by higher betas, tend to consist of smaller firms. We are not aware of any empirical evidence that demonstrates that risky industries (with higher betas) tend to consist of smaller firms. In fact, the evidence seems to show no correlation between industry beta and firm size.
If one views Dr. Aswath Damodaran’s industry betas, we see that multiple industries having higher betas almost certainly tend to have bigger firms, not smaller—for example, the beverage (alcoholic) industry, with a beta of 1.30 as of January 2019; beverage (soft), with a beta 1.18; brokerage and investment banking, with a beta of 1.21; chemical (diversified), with a beta of 1.82; and drugs (pharmaceutical), with a beta of 1.47; among others. This evidence in Dr. Damodaran’s data library appears to indicate there is no correlation between industrywide risk factors, subsumed as industry beta, and firm size.
Q: When using the capital asset pricing model (CAPM), should I use the “Size Premium (S&P 500)” or the “Size Premium (Beta Adjusted)”?
A: If the analyst decides to use a size premium, then the “Size Premium (Beta Adjusted)” would be appropriate when using the capital asset pricing model in estimating cost of equity if the analyst believes smaller firms tend to have higher CAPM betas. In such cases, using a beta-adjusted size premium in a CAPM rather than “Size Premium (S&P 500)” would likely avoid some duplication of risk already captured in the particular model’s beta.
Q: Does the Cost of Capital Professional platform include subdivisions of the 10th decile holding smaller listed firms? If not, why?
A: No. Returns of smaller listed firms likely have multiple factors affecting their returns other than firm size. In general, smaller listed firms are small for reasons such as firm characteristics of poor profitability, cash flow problems, financial distress risk, or high leverage. Such characteristics of smaller listed firms may differ from those of unlisted firms being valued making simple inferences from smaller listed firms to unlisted firms possibly unreliable. See, for example:
- Chan, K. C., & Chen, N.-F. (1991). Structural and Return Characteristics of Small and Large Firms. Journal of Finance, 46(4), 1467-1484.
- Asness, C., Frazzini, A., Israel, R., Moskowitz, T. J., & Pedersen, L. H. (2018). Size matters, if you control your junk. Journal of Financial Economics, 129(3), 479-509.
Also note from Valuing a Business (6th ed.), Shannon Pratt and ASA Educational Foundation (2022) pg. 244. New York: McGraw-Hill:
“Troubled companies make up many the companies included in 10b; their market values are trading as call options, causing the beta measurement problem.”
And note from PPC’s Guide To Business Valuations, Practitioners Publishing Business, 31st Edition: sections 505.34 – 505.35:
“505.34 Although this further split of the 10th decile is interesting, the consultant needs to be mindful of its limitations. These limitations apply not only to 10w, 10x, 10y, and 10z subcategories, but also to the initial splitting into 10a and, more particularly, 10b.
505.35 Since Ibbotson split the 10th decile into 10a and 10b, many valuation consultants have questioned sole reliance on 10b, as it is always significantly higher than 10a and 10. Some consultants believe the significantly higher size premium for 10b is further proof of the size phenomenon. However, other consultants reason that the difference can be ascribed to the inclusion of startup companies and distressed companies, whose market capitalization is small because they are speculative and distressed. For this reason, many practitioners use only the 10th decile or the expected micro-capitalization equity size premium, which includes both 9th and 10th deciles. Another issue to consider is the number of companies in the 10th decile over time. There were only 52 companies in all the 10th decile in 1926, which is the starting point for the use of Ibbotson data for many analysts. It was not until the 1960s that the number of 10th decile companies reached over 100, which means the number of 10z companies is much less. As such, the number of companies in a significant amount of the time period for the calculation of the size risk premium is much less than in latter years.”
Q: Is there a list for the industry/sectors used in the Industry Risk Premium (IRP)?
A: Yes. For Dr. Aswath Damodaran's data, you can find the company lists here (select "download detail"). For the Salvidio & Partners data, the company lists can be requested here.
Q: How can I search the industry betas when retrieving an IRP?
A: Dr. Aswath Damodaran’s data can be searched using a dropdown list or by keyword text. Salvidio & Partners data can be searched by dropdown list, keyword text, or SIC code. Note that using SIC will produce the closest match possible from the available industries, but may not always produce an exact match. For example, a search for 5812 will retrieve Restaurants while a search for 5813 will also retrieve Restaurants, as there is no available drinking location/bar industry.
Q: I am trying to reconcile the historical equity risk premiums and sizes premiums reported in the Cost of Capital Professional with those from another source and I am finding that they are different. Can you please explain why?
A: In short, in measuring historical equity risk premiums and size premiums, part of the difference is attributed to methodology, while another part may be due to differences in the data sources used.
The Cost of Capital Professional relies on historical return data from CRSP. The Cost of Capital Professional measures historical ERP as:
Mean return of the CRSP’s S&P 500 Universe minus mean return of Treasury bonds (please see definition for “CRSP – Historical ERP” toward the top of the FAQ page).
CRSP measures monthly bond returns for a Treasury bond from the monthly price change plus interest, divided by last month’s price (please see CRSP 1925 Historical Indexes Guide, p. 9).
The Size Premium (S&P 500) compares the mean decile return to the S&P 500 mean return and takes the difference as an estimate of the decile size premium. Put differently, the Size Premium (S&P 500) measure is the average extra decile return over the average S&P 500 return.
The S&P 500 is a proxy for the market portfolio used in the equity risk premium.
The Size Premium (Beta Adjusted) uses a CAPM methodology to estimate size premiums. Since smaller firms have higher betas on average, size premiums for smaller firms using this methodology tend to be lower because a larger beta absorbs some of the extra decile return relative to the S&P 500 return.
Q: Why does the Cost of Capital Professional use total returns for the Treasury bond when calculating the Equity Risk Premium?
A: The concept of the equity risk premium is the extra return that investors earn by owning risky stocks over the return by owning a risk-free asset. The formulation of this concept can be expressed as:
Return of risky stocks minus the return of a risk-free asset = Extra return of risky stocks
Assuming one develops the equity risk premium from historical data, they likely assume the future will resemble the past, on average. The formulation of the equity risk premium using historical return data can be expressed as:
Actual return by owning risky stocks at time t minus actual return by owning a risk-free asset at time t = Historical extra return by owning risky stocks at time t
If one measures historical returns annually, then observe the actual return of stocks and the actual return of a risk-free asset for each year. The return measures are what investors actually earned that year and the measures are objective. Then determine the difference between the two returns for each year. To determine the average annual extra return of risky stocks over a risk-free asset, then sum the annual return differences across all years and divide by the number of years. Moreover, using only a portion of the actual return of a risk-free asset (e.g., excluding the capital appreciation portion) is an incomplete measure of what investors actually earned. If one is basing their analysis on objective observation, then observe what investors actually earn in total by holding an asset. Doing anything else introduces some degree of subjectivity.
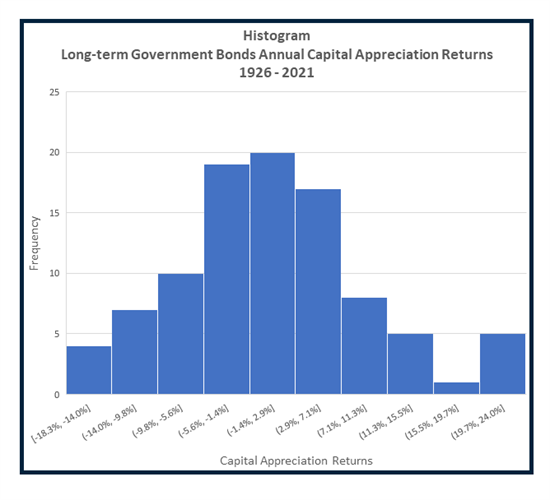
The data shows that long-term government bonds have capital appreciation returns close to zero over the long run. Kroll explicitly reports historical capital appreciation returns of long-term government bonds since 1926 (Kroll, 2022 SBBI Yearbook, Stocks, Bonds, Bills, and Inflation, Appendix A-8 (Long-term Government Bonds: Capital Appreciation Returns)). For 1926-2021, the mean annual capital appreciation return is 0.88% and the standard error is 0.91%. Statistically, bonds have had no capital appreciation return since 1926. This empirical observation is consistent with what we know about the prices of seasoned government bonds and interest rates. When interest rates fall (rise), seasoned bond prices (capital appreciation) rise (fall). Interest rates famously are hard to predict. Interest rates go up and down. Capital appreciation returns go up and down. For 1926-2021, annual capital appreciation returns were down about one-half the years and up about one-half the years. The plot below is a histogram of annual capital appreciation returns from 1926 through 2021.
If one uses T-bonds as a risk-free asset instead of T-bills to value a business, they implicitly assume an investment in the company will be held by an investor(s) for a longer period of years. As described, long-term government bonds have no capital appreciation return over the long run. If you believe that interest rates will rise between now until the time a seasoned T-bond matures in, say, 10 or 20 years, then you will experience negative capital appreciation but, interest rates go up and down. Even if they go up, they will certainly go down sometime later. If one uses historical return data to derive the equity risk premium for valuing a business investment and holding it for a longer period, it is statistically more reliable to use historical data over multiple decades rather than shorter periods (unless something has structurally changed that affects returns).
Q: How does the Cost of Capital Professional platform measure firm size for the size premium?
A: The Cost of Capital Professional platform presents return data across firm sizes with size measured as the market value of equity (market capitalization). This measure is very likely the most common measure of firm size in academic research on the cross-section of equity returns (see, for instance, Yakov Amihud and Haim Mendelson, “The Effects of Beta, Bid-Ask Spread, Residual Risk, and Size on Stock Returns,” Journal of Finance, 1989, 44:479-86; Eugene F. Fama and Kenneth R. French, “The Cross-Section of Expected Stock Returns,” Journal of Finance, 1992, 47:427-65; Eugene F. Fama and Kenneth R. French, “Common Risk Factors in the Returns on Stocks and Bonds,” Journal of Financial Economics, 1993, 33:3-56; and Mark M. Carhart, “On Persistence in Mutual Fund Performance, Journal of Finance, 1997, 52:57-82). Use of market value of equity for firm size is market-oriented and captures forward-looking expectations of market participants.
In contrast to research using market value of equity for firm size, academic studies using nonmarket measures for size (e.g., book value of assets, annual sales, number of employees) show no size premium in smaller listed firms not otherwise predicted by CAPM (see, for instance, Ron Alquist, Ronen Israel, and Tobias Moskowitz, “Fact, Fiction, and the Size Effect,” The Journal of Portfolio Management, 2018, 45 (1):34-61. doi: doi.org/10.3905/jpm.2018.1.082. See also, Jonathan B. Berk, “An Empirical Re-Examination of the Size Relation Between Firm Size and Returns,” working paper, University of Washington, 1996; and Jonathan B. Berk, “Does Size Really Matter?” Financial Analysts Journal, 1997, 53(5): 12-18.)
Q: What are the options for the “Returns Reference – End Year” field?
A: The provided options are dependent on the analyst’s entry in the “Valuation Date” field. Generally, the provided year will be the valuation date year - 1 year. For a valuation date in 2019, for instance, the provided end year will be 2018 unless the Q4 2018 CRSP data have not yet been published.
For valuation dates in December, the provided options are the valuation date year - 1 and, if available at the time of user access, the valuation date year. For instance, a valuation date in December 2018 will have year-end options of 2017 and, if available at the time of user access, 2018.
For valuation dates in January and February, the provided options for the valuation date year - 1, if available at the time of user access, and the valuation date year - 2, For instance, a valuation date of Jan. 15, 2019, will have year-end options of 2018, if available at the time of user access, and 2017.
Q: Will you please explain the Implied ERP and the Implied ERP With Sustainable Payout?
A: Dr. Aswath Damodaran, a professor of corporate finance and valuation at the Stern School of Business at New York University, calculates both the Implied ERP and the Implied ERP With Sustainable Payout. Implied ERP is a forward-looking measure ERP based on observed current market information rather than an average of past returns over decades. For more information, please read “Equity Risk Premiums (ERP): Determinants, Estimation and Implications – The 2018 Edition.”
Q: Dr. Aswath Damodaran expresses his implied ERP as a geometric measure (Aswath Damodaran, "Equity Risk Premium (ERP): Determinants, Estimation and Implications - The 2018 Edition," 2018). Since implied ERP is not derived from a time series, how does the Cost of Capital Professional convert his geometric measure to an arithmetic measure of implied ERP?
A: The arithmetic return approximately equals the geometric return plus half the variance (see, for instance, Richard A. DeFusco, Dennis W. McLeavey, Jerald E. Pinto, and David E. Runkle, Quantitative Methods for Investment Analysis, 2nd ed., Charlottesville, Va.: CFA Institute, 2004, ch. 3). The Cost of Capital Professional uses the historical average variance of the S&P 500 returns over the user-selected start and end dates and applies this formulation to Dr. Aswath Damodaran's geometric implied ERP. (The standard deviation of the S&P 500 returns from 1928 to 2017, for instance, was 18.9%.)
Q: Along with the 10 CRSP decile size premiums, does the Cost of Capital Professional platform provide any other size premiums figures?
A: Yes. It provides historical size premiums for the following combined portfolio groups: micro-cap (deciles 9-10), small-cap (deciles 6-8), mid-cap (deciles 3-5), and large-cap (deciles 1-2).
Q: Are there any online resources for industry CAPM betas that I could use to populate the CAPM beta field for the firm being valued?
A: Yes. Dr. Aswath Damodaran publishes current industry betas here and archived historical betas here.
Salvidio & Partners publishes industry betas quarterly for 65 industries and 144 sub-industries. BVR makes current and historical reports available to subscribers here.
Q: Are there any online resources for company-specific risk premiums (CSRPs) that I could use to populate the CSRP field?
A: BVR offers the Butler Pinkerton Calculator, an empirical resource for determining CSRPs, which can be used in conjunction with professional judgment.
Q: Am I able to select my own values for the risk-free rate and equity risk premium?
A: Yes. You can enter your own values for the risk-free rate and equity risk premium if you wish. You are also provided with an accompanying field to enter any notes that may be associated with your selection.
Q: Am I able to save any of my cost of equity calculations to revisit at a later date?
A: Yes. You can save your calculation by selecting the “Save” option in the upper-right corner of the tool. When saving your work, you have the ability to provide a unique name for your saved work, as well as a space to include any notes that may be associated with your saved calculation. You can revisit all of your saved calculations at any time by selecting the “Recent” option in the upper-right corner of the tool.
Please note: All saves are retained for one year. It is recommended that you download, save, or otherwise retain your work outside of solely saving it from within the platform.
Q: What are the outputs of the Cost of Capital Professional platform?
A: One output is a summary of your cost of equity estimates that can easily be copied and pasted into your work product using the “Copy” selection on the “Summary” tab.
Another output is an Excel download to export all of your selected variables, documentation, sources, notes, and calculations. This is available under the “Download” tab.
Q: My subject company is smaller than the companies in the 10th decile (the smallest listed companies). Which size premium should I select?
A: The data for the 10th decile provide premium information for the smallest listed firms (based on market capitalization). An adjustment to the 10th decile size premium may be appropriate for smaller unlisted firms based on the analyst’s professional judgment.
Q: Can the Cost of Capital Professional platform be used for non-U.S.-based companies?
A: Generally, one would want to use risk premia developed using U.S. data for valuations of U.S.-based firms. The data for the Cost of Capital Professional platform are on firms listed on U.S. stock exchanges. Equity risk premium and size premium measures are the results of these U.S. data. For valuations of firms in other countries, the analyst should carefully assess whether U.S. data are useful for his or her valuation or could be adapted to his or her location.